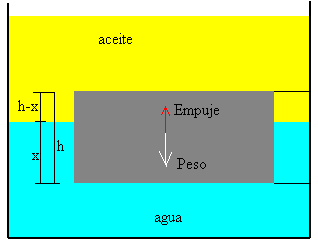
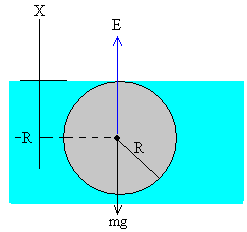
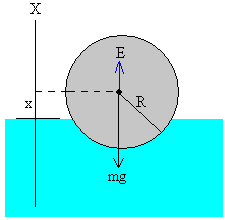
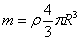Desde la antigüedad , el ser humano se ha cuestionado de que estaba hecha la materia.
Unos 400 años antes de Cristo , el filosofo griego Democrito considero que la materia estaba constituida por pequeñísimas partículas que no podían ser divididas en otras mas pequeñas . Por
ello , llamó a estas partículas átomos , que en griego quiere decir "indivisible" . Democrito atribuyo
a los átomos las cualidades de ser eternos , inmutables e indivisibles .
Sin embargo las ideas de Democrito sobre la materia no fueron aceptadas por los filósofos de su
época y hubieron de transcurrir cerca de 2200 años para que la idea de los átomos fuera tomada de nuevo en consideración .

ESTRUCTURA DEL ATOMO
En el átomo distinguimos dos partes : el núcleo y la corteza .
El núcleo es la parte central del átomo y contiene partículas con carga positiva , los protones , y
partículas que no poseen carga eléctrica , es decir son neutras , los neutrones . La masa de un proton es aproximadamente igual a la de un neutron .
Todos los átomos de un elemento químico tienen en el núcleo el mismo numero de protones . Este numero , que caracteriza a cada elemento y lo distingue d los demás , es el numero atómico y se representa con la letra Z .
La corteza es la parte exterior del átomo . En ella se encuentran los electrones , con carga negativa .
Estos , ordenados en distintos niveles , giran alrededor del núcleo . La masa de un electrón es unas 2000 veces menor que la de protón .
Los átomos son electricamente neutros , debido a que tienen igual numero de protones que de electrones . Así , el numero atómico tambiém coincide con el numero de electrones .

La suma del número de protones y el número de neutrones de un átomo recibe el nombre de número másico y se representa con la letra A .
Para representar un átomo , hay que indicar el número másico (A) y el número atómico (Z) , colocados como índice y subíndice , respectivamente , a la izquierda del símbolo del elemento .